Vamos iniciar este assunto fazendo uma analogia com o conceito já conhecido de energia potencial gravitacional.

O POTENCIAL GRAVITACIONAL

Consideremos dois pontos A e B, próximos a superfície da Terra, e portanto sob influencia do campo gravitacional da mesma. Veja a figura abaixo:

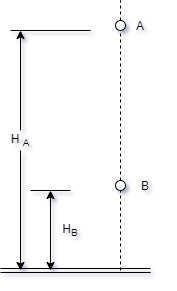
Sabemos que um corpo qualquer, de massa m, colocado nesses pontos, adquire energia potencial gravitacional, que pode ser calculada pela relação E_p = m.g.h

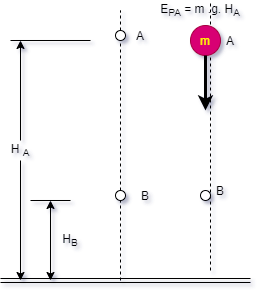
Um corpo de massa m adquire energia potencial gravitacional E_p = m.g.h, ao ser colocado, por exemplo, no ponto A.

Vamos calcular o trabalho realizado pelo peso P, do corpo, ao deslocá-lo do ponto A até o ponto B.

A aceleração da gravidade será admitida constante, e DH = H_A - H_B.

Temos: W_AB= F x d  ==> W_AB= P x DH   ==> W_AB= m.g x  (H_A - H_B)

W_AB= m.g.H_A- m.g.H_B

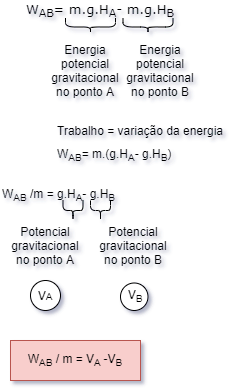
A relação V = g.H é, por definição, chamada  de potencial gravitacional.

Note que para determinar a energia potencial gravitacional de um corpo, basta multiplicar a massa deste corpo pelo potencial do ponto.

O POTENCIAL ELÉTRICO.

Vamos admitir, inicialmente, uma determinada região do espaço, onde exista um campo elétrico uniforme, representado por sua linhas de força, paralelas e igualmente espaçadas. Consideremos dois pontos A e B, deste campo.

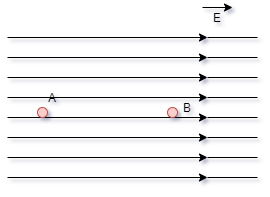
Um campo elétrico uniforme é representado geometricamente por retas paralelas igualmente espaçadas.

Coloquemos, no ponto A, em repouso, uma partícula carregada eletricamente, com uma carga positiva q+. E fácil perceber que aparecerá, na carga, uma força elétrica constante F = q.E.

Sob efeito da força F, a partícula se deslocará naturalmente do ponto A até o ponto B, percorrendo a distância d. O trabalho realizado por F é:

W_AB = F.d  => E = F/q  => F = E.q

logo W_AB = E.q.d  ==> W_AB/q = E.d

Por analogia com o potencial Gravitacional  W_AB/m => W_AB/q

Podemos definir que  W_AB/q = E.d = V_A - V_B

Observações importantes.:

Na figura abaixo, duas cargas elétricas q₁⁺ e q₂^-, estão sob efeito de um campo elétrico uniforme.

A carga de prova (q₁⁺) se desloca do ponto A para um ponto B naturalmente, e diremos que o potencial do ponto A é mais elevado é mais elevado que o potencial do ponto B.

1- A carga elétrica positiva se desloca naturalmente do potencial mais alto para o potencial mais baixo.

2- A carga elétrica negativa se desloca naturalmente do potencial mais baixo para o potencial mais alto.

3- O potencial elétrico é uma grandeza física escalar. Pela própria definição, é fácil verificar tal observação:

V_AB = W_AB/q   W_{AB =>} Escalar      q = Escalar  logo V_AB = Escalar

4- Unidade de potencial

W/q = V   => joule/ Coulomb = volt (V).

O potencial elétrico de uma carga puntiforme

         Inicialmente, é necessário salientar que sendo o potencial elétrico uma grandeza física escalar, deve-se levar em consideração o sinal da carga elétrica reproduz o potencial, isto quer dizer  quê potencial de carga positiva é positivo e potencial de carga negativa é negativo.

          Consideremos, então, uma carga puntiforme, positiva, isolada e fixa em determinada região do espaço a figura que se segue mostra dois pontos A e B , de uma das linhas de força do campo elétrico que provoca e uma carga positiva, de prova, colocada em repouso em A.

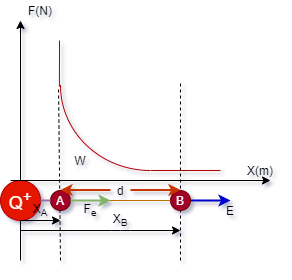
             Sobre a Carga de prova q positiva, aparece a força elétrica F, que a faz deslocar-se do ponto A em direção ao ponto B, ao longo da linha de força. Vamos calcular o trabalho realizado por essa força entre os pontos aA e B.

              É evidente que a relação w = f.d não pode ser utilizada neste caso, pois representa o trabalho de uma força constante.  Como já sabemos, a força elétrica entre as duas cargas é uma função da distância entre elas (F∞ 1/d²).

             Assim sendo no caso de campos elétricos variáveis, que provocam também forças variáveis, o cálculo da diferença de potencial entre dois pontos desse campo é feito com auxílio do cálculo integral.

             Para a carga puntiforme podemos demonstrar que:                       

o quê observe que a área indicada não é ou melhor é arrumar figura geométrica regular conhecida o cálculo dessa área é feito através de cálculo integral o potencial elétrico em um ponto p qualquer de um campo elétrico produzido por uma carga puntiforme pode ser determinado pela relação o potencial resultante a figura que se segue mostra uma região do espaço ço isso essa simultânea de 3 cargas elétricas puntiformes quer um que é 23 cada uma dessas cargas produz no ponto p potencial particular sendo potencial busca lá o potencial resultante em p é a somar um chereca desses valores parciais

Exercícios e problemas (Potencial Elétrico)

1. Uma certa bateria de automóvel de 12 V pode enviar uma carga total  84 A-h(ampéres-hora)através de um circuito, de um terminal ao outro. (a) Quantos coulombs de carga isso representa?(Dica: Veja a Eq. 22.3) (b) Se toda esta carga estiver sujeita a uma diferença de potencial de 12 V, qual a energia envolvida?

(a) Um Ampere é um Coulomb por segundo, então
84 A · h = 84 C · h/s  3600s/h = 3,0 x 10⁵ C.
(b) A mudança na energia potencial é ∆U = q ∆V = (3,0 × 10⁵ C) (12 V) = 3,6 × 10⁶ J.

2. A diferença de potencial elétrico entre o solo e uma nuvem em uma determinada tempestade é de 1,2 x 10⁹V. Qual a intensidade da variação da energia elétrica (em múltiplos do elétron - volt) de um elétron que se move entre o solo e a nuvem?

A intensidade é ∆U = e∆V = 1,2 × 10⁹ eV = 1,2 GeV.

3. Em um determinado relâmpago, a diferença de potencial entre uma nuvem e o solo é de 1,0 x 10⁹ V e a quantidade de carga transferida é de 30 C. (a) Qual a redução na energia dessa carga transferida?(b) Se toda essa energia pudesse ser usada ser usada para acelerar um automóvel de 1000 kg a partir do repouso, qual seria a velocidade final do automóvel?(c) Se a energia pudesse ser usada para derreter gelo, quanto gelo ela derreteria a 0ºC?O calor de fusão do gelo é igual a 3,33 x 10⁵ J//kg.

Quando a carga q se move através de uma diferença de potencial ∆V, sua energia potencial muda ∆U = q ∆V. Neste caso, ∆U = (30 C) (1,0 × 10⁹ V) = 3,0 × 10¹⁰ J.
(b)Igualando a energia cinética final 1/2mv² do automóvel a energia liberada pelo raio, v = √2.∆U/m.  => √2 (3,0 × 10¹⁰ J)/1000 kg = 7,7 x 10³ m / s.

(c) Igualando a energia necessária para derreter a massa m de gelo a energia liberada pelo raio:
∆U = mLF, onde LF é o calor da fusão para gelo. Portanto,

m = ∆U/LF = 3,0 × 10¹⁰ J / 3,33 × 10⁵ J / kg = 9,0 × 10⁴ kg.

4. Quanto um elétron se move de A para B ao longo de uma linha de campo elétrico na fig. 25.29, o campo elétrico realiza sobre ele 3,94 x 10^-19J de trabalho. Quais as diferenças de potencial elétrico (a) V_B - V_A, (b) V_C - (c) V_C-V_B?

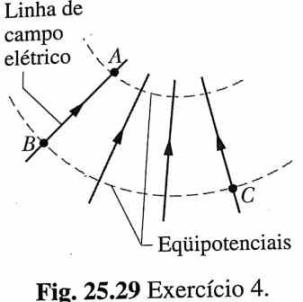
(a) V_B - V_A = ∆U / (- e) = (3,94 × 10⁻¹⁹ J) / (- 1,60 × 10⁻¹⁹ C) = −2,46 V.
(b) V_C - V_A = V_B - V_A = −2,46 V.
(c) V_C - V_B = 0 (já que C e B estão na mesma linha equipotencial).

5. Uma placa não-condutora infinita possui uma densidade superficial de carga s = 0,10 µC/m² sobre um dos lados. Qual a separação entre as superfícies equipotenciais cujos potenciais diferem de 50 V?

O campo elétrico produzido por uma folha infinita de carga tem intensidade E = σ / 2ε₀, onde σ é o densidade de carga superficial. O campo é normal para a folha e é uniforme. Coloque a origem de uma coordenada sistema na folha e tomar o eixo x para ser paralelo ao campo e positivo na direção do campo. Então o potencial elétrico é

                _x
V = Vs -∫0  E dx = Vs - Ex,

onde Vs é o potencial na folha. As superfícies equipotenciais são superfícies de constante x; isso é, são planos paralelos ao plano de carga. Se duas superfícies são separadas por x, então seus potenciais diferem em magnitude por ∆V = E∆x = (σ / 2ε₀) ∆x. Portanto,

∆x = 2ε0 ∆V/σ = 2(8,85 × 10^-12 C² / N · m²)(50 V)/0,10 × 10⁻⁶ C / m² = 8,8 × 10⁻³ m.

6. Duas grandes placas condutoras paralelas estão distantes 12 cm uma da outra e possuem cargas de mesma intensidade e sinais contrários sobre suas superfícies vizinhas. Uma força eletrostática de 3,9 x 10^-15 N atua sobre um elétron colocado em um lugar qualquer entre as duas placas. ( Despreze o efeito de borda) (a) Determine o campo elétrico na posição do elétron. (b) Qual a diferença de potencial entre as placas?

(a) E = F/e = (3.9 × 10⁻¹⁵ N)/(1.60 × 10⁻¹⁹ C) = 2.4 × 10⁴ N/C.
(b) ∆V = E∆s = (2.4 × 10⁴ N/C)(0.12 m) = 2.9 × 10³ V.

7. Considere uma carga pontual q = 1,0 µC, um ponto A a uma distância d₁ = 2,0 m de q e um ponto B a uma distância d₂ = 1,0 m. (a) Se estes pontos estiverem diametralmente opostos um do outro, como na Fig. 25. 31a, qual a diferença de potencial elétrico V_A - V_B?(b) Qual será essa diferença de potencial elétrico se os pontos A e B estiverem localizados como na fig. 25.31b?

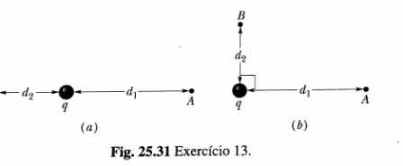
(a) A diferença de potencial é V_A - V_B = q/4πε₀r_A - q/4πε₀r_B

= (1,0 × 10⁻⁶ C)(8,99 × 10⁹ N · m² / C² ) (1/2,0 m - 1/1,0 m) = −4500 V.

(b) Como V (r) depende apenas da magnitude de r, o resultado é inalterado.

8. Na fig. 25.32, considere V = 0 no infinito e que as partículas tenham cargas q₁ = +q e q₂ = -3q. Localize então (em termos de distância de separação d) um ponto qualquer sobre o eixo x ( que não esteja no infinito) no qual o potencial devido as duas partículas seja nulo.

Primeiro, observamos que V (x) não pode ser igual a zero para x> d. De fato, V (x) é sempre negativo para x> d.
Agora consideramos as duas regiões restantes no eixo x: x <0 e 0 <x <d. Para x <0 a separação entre q₁ e um ponto no eixo x cuja coordenada é x é dada por d₁ = −x; enquanto o correspondente separação para q₂ é d₂ = d - x. Montamos
V (x) = k(q₁/d₁ + q₂/d₂) = q/4πε₀ (1/−x + −3/d - x) = 0
para obter x = −d / 2. Similarmente, para 0 <x <d temos d₁ = x e d₂ = d - x. Deixei

V (x) = k(q₁/d₁ + q₂/d₂) = q/4πε₀ (1/x + −3/d - x) = 0

resolvendo: x = d / 4.

9. Duas partículas com cargas q₁ e q₂ estão separadas pela distância d na fig. 25.32. O campo elétrico resultante das partículas é nulo em x = d/4. Com V = 0 no infinito, localize (em termos de d ) um ponto qualquer sobre o eixo X ( que não seja no infinito) no qual o potencial elétrico devido as duas partículas seja nula.

Uma vez que, de acordo com a colocação do problema, existe um ponto entre as duas cargas no eixo x onde o campo elétrico líquido é zero, os campos naquele ponto devido a q₁ e q₂ devem ser direcionados opostos
uns aos outros. Isso significa que q₁ e q₂ devem ter o mesmo sinal (ou seja, ambos são positivos ou ambos negativos). Assim, os potenciais devidos a qualquer um deles devem ser do mesmo tipo. Portanto, o potencial elétrico não pode ser zero em lugar algum, exceto no infinito.

10. Uma gota de d' água esférica transportando uma carga de 30 pC possui um potencial de 500 V na sua superfície (com V = 0 no infinito). (a) Qual o raio da gota?(b) Caso duas gotas como esta, com mesma carga e raio, se combinarem para formar uma única gota esférica, qual será o potencial na superfície da nova gota?

(a) O potencial elétrico V na superfície da gota, a carga q, e o raio R está relacionada por V = q / 4πε₀R. portanto

R = q/4πε₀V = (8,99 × 109 N · m² / C²)(30 × 10^-12 C)/500 V = 5,4 × 10⁻⁴ m.

(b) Depois que as gotas combinam, o volume total é o dobro do volume de uma gota original, então o raio R combinado é dada por

(R') ³ = 2R³ e R' = 2^1/3R. A carga é o dobro da carga original:    q' = 2q. Portanto,
V' = 1/4πε_{0 .}q'/R' = 1/4πε₀ 2q/2^1/3R = 2^2/3V = 2^2/3 (500 V) ~ 790 V.

11. Quais (a) a carga e (b) a densidade de carga na superfície de uma esfera condutora de raio 0,15m, cujo potencial é 200V ( com V = 0 no infinito)?

12. Observa-se com frequência um campo elétrico de aproximadamente 100 V/m próximo a superfície da terra. Se este fosse o campo sobre toda a superfície terrestre, qual seria o potencial elétrico de um ponto sobre a superfície?(Considere V = 0 no infinito.)

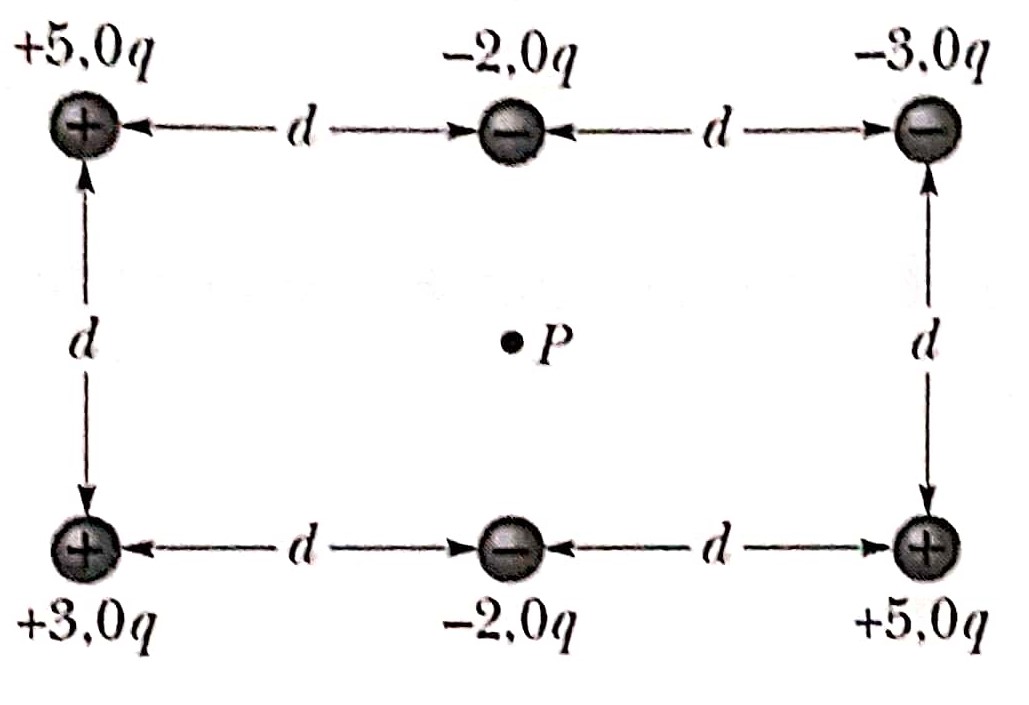
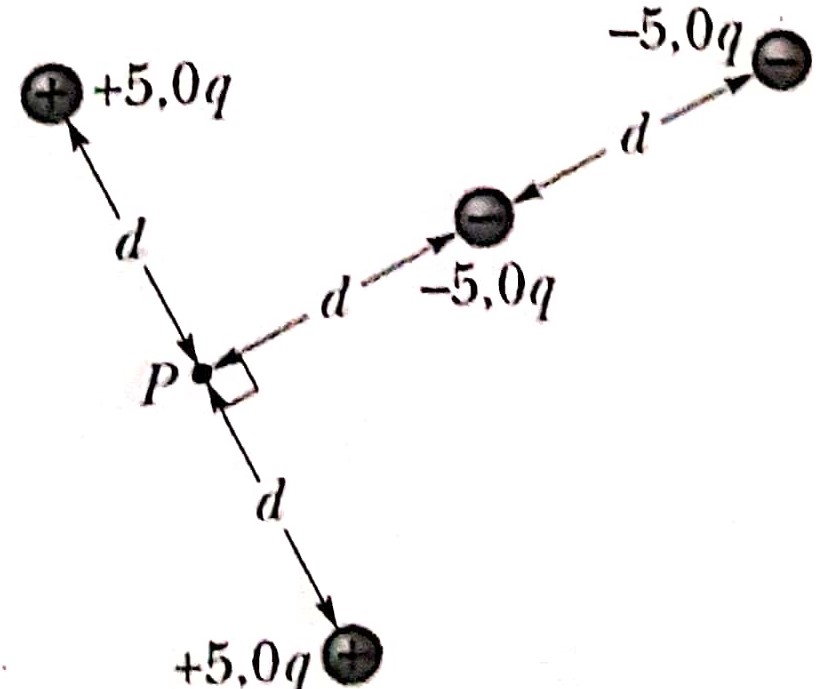
13. Na figura abaixo o ponto P está no centro do retângulo. Com V = 0 no infinito, qual o potencial resultante em P devido as seis partículas carregadas?

14. Na figura abaixo, qual o potencial resultante no ponto P devido as quatro cargas pontuais, se V = 0 no infinito?

15. Duas grandes placas metálicas paralelas estão afastadas uma da outra 1,5 cm e possuem cargas iguais mas contrárias sobre suas superfícies vizinhas. Considere o potencial da placa negativa como nulo. Se o potencial no meio da distância entre as placas é então de + 5,0 V, qual o campo elétrico na região entre as placas?

16. O potencial elétrico em pontos de um plano xy é dado por V = (2,0 V/m²)x² - (3,0 V/m²)y². Qual a intensidade , direção e sentido do campo elétrico no ponto (3,0 m, 2,0 m)?

17. O potencial elétrico V no espaço entre duas placas planas paralelas é dado por V = 1500x², onde V está em volts se x, a distância a uma das placas, estiver em metros. Calcule a intensidade, direção e sentido do campo elétrico em X = 1,3 cm.

18. (a) Qual a energia potencial elétrico de dois elétrons separados de 2,00nm?(b)Se a separação aumentar ,a energia potencial aumentará ou diminuirá?

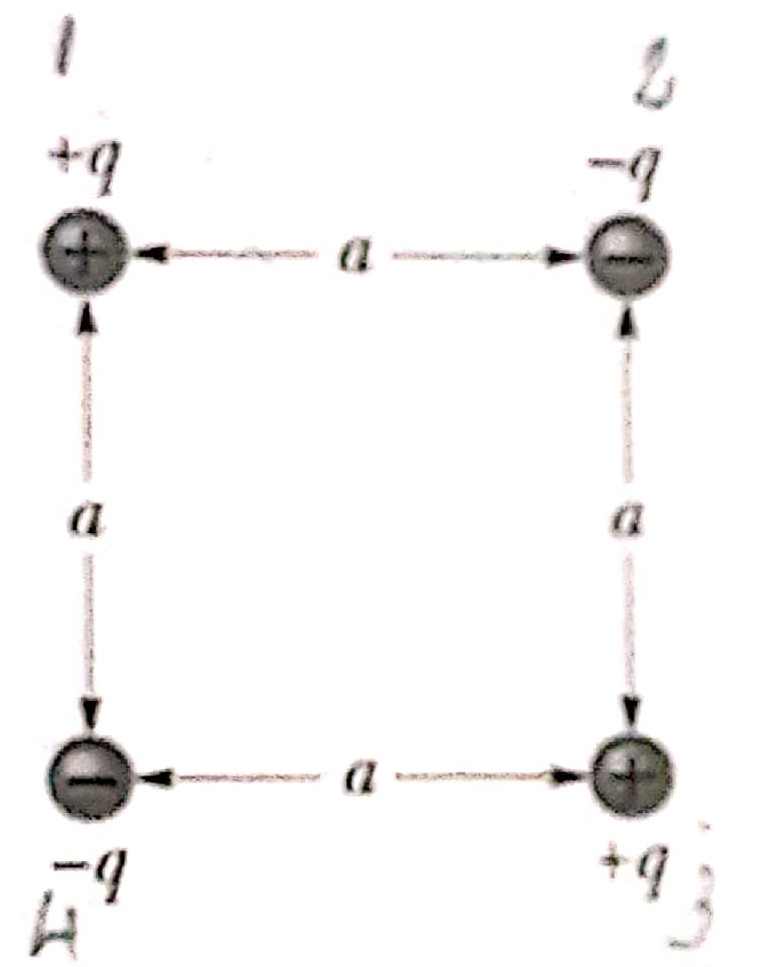
19. Deduza uma expressão para o trabalho exigido para estabelecermos a configuração de quatro cargas da fig. 25.41, supondo que as cargas estejam inicialmente separadas por uma distância infinita.

20. Qual a energia potencial elétrico da configuração de carga da fig. 25.9a?Use os valores numéricos fornecidos no problema resolvido 25.3.

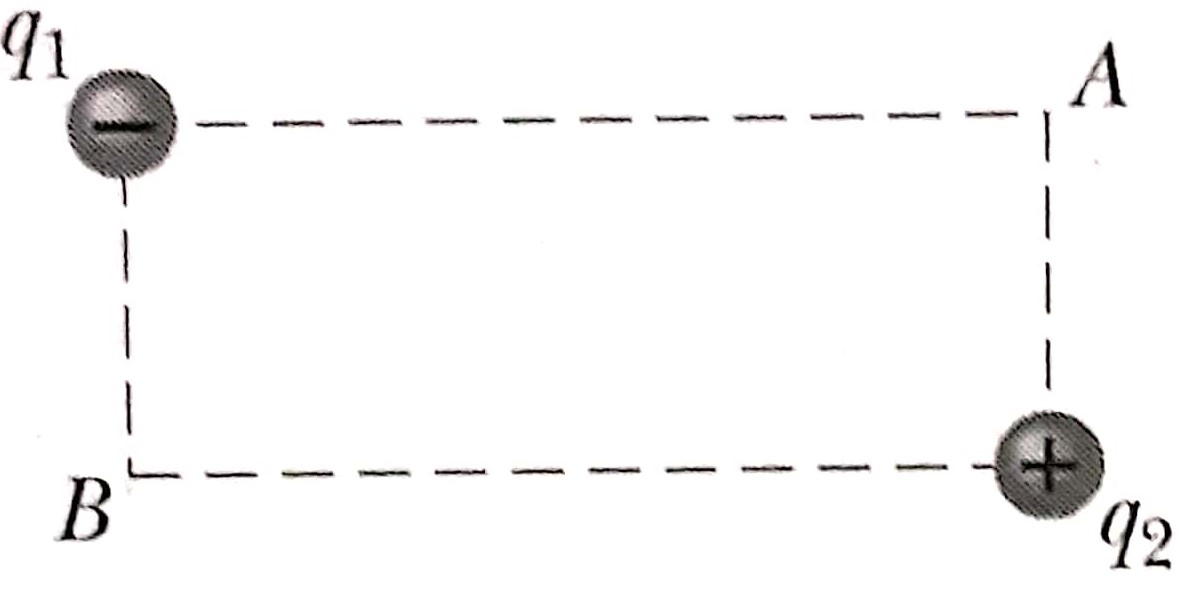
21. No retângulo da figura abaixo, os lados possuem comprimentos de 5,0cm e 15cm, q₁ = -5,0µC e q₂ = +2,0 µC. Com V = 0 no infinito, quais os potenciais elétricos (a) no vértice A e (b) no vértice B?(c) Qual o trabalho necessário para mover uma terceira carga q₃ = +3,0µC de B para A ao longo de uma diagonal do retângulo?(d) Este trabalho aumenta ou diminui a energia elétrica do sistema de três cargas?Este trabalho é maior, menor ou o mesmo exigido se q₃ for movida ao longo de trajetórias que estejam (e) dentro do retângulo, mas não sobre uma diagonal , e (f) fora do retângulo?

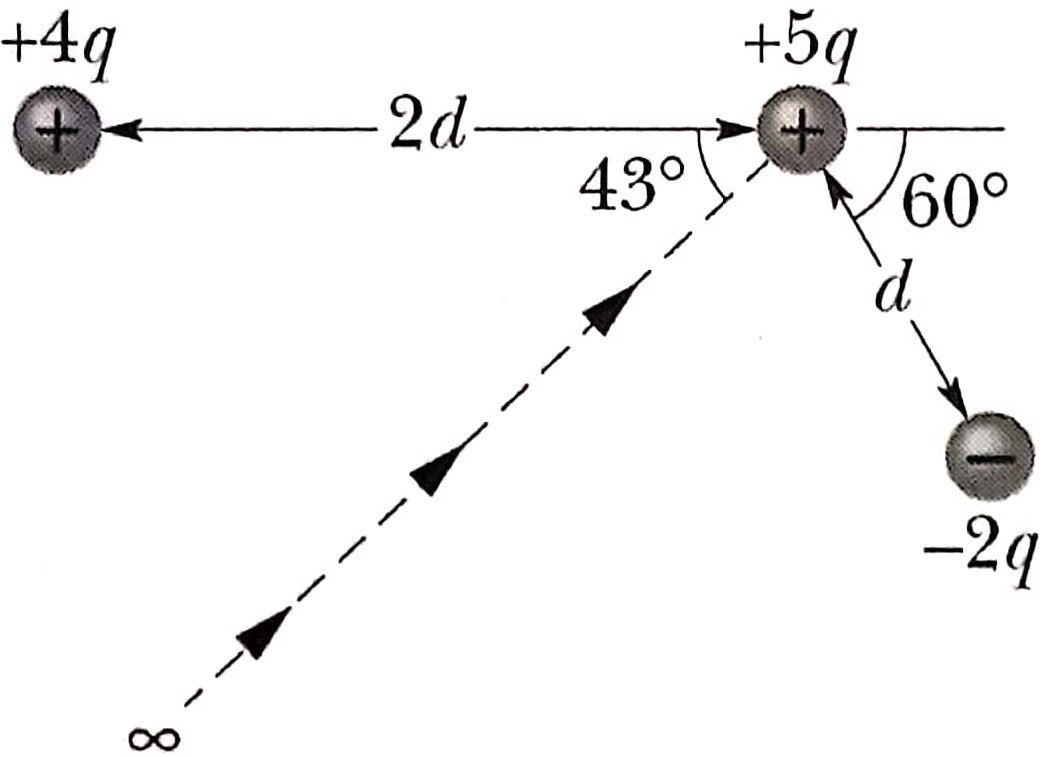
22. Na figura abaixo, qual o trabalho exigido para trazer a carga de +5q do infinito ao longo da linha tracejada e colocá-la, como mostra, como mostrado, próximo as duas cargas fixas + 4q e - 2q? Adote a distância d = 1,40 cm e a carga q = 1,6 x 10^-19C.

23. Uma partícula de carga q está fixa no ponto P e uma segunda partícula de massa m e mesma carga q é mantida inicialmente a uma distância r₁ de P. A segunda partícula é então solta. Determine sua velocidade quando ela estiver a uma distância r₂ de P. Considere q = 3,1 µC,m = 20mg, r₁ = 0,90 mm e r₂ = 2,5mm.

24. Duas esferas metálicas minúsculas A e B de massa m_A = 5,00g e m_B = 10,0g possuem cargas positivas iguais q = 5,00µC. As esferas estão ligadas por um fio não - condutor e de massa desprezível de comprimento a = 1,00 m, que é muito maior do que os raios das esferas. (a) Qual a energia potencial elétrica do sistema?(b) Suponha que você corte o fio. Nesse instante, qual a aceleração de cada esfera?(c) Muito tempo depois de você ter cortado o fio, qual a velocidade escalar de cada esfera?

25. Dois elétrons estão fixados com uma separação de 2,0 cm entre eles. Um outro elétron é disparado do infinito e pára na metade da distância entre eles. Qual a sua velocidade escalar inicial?

26. Uma esfera metálica oca vazia possui um potencial de +400V em relação ao solo ( definido como V = 0 ) e possui uma carga de 5,0 x 10^-9C. Determine o potencial elétrico no centro da esfera.

27. Qual a carga em excesso sobre uma esfera condutora de raio r = 0,15m se o potencial da esfera for de 1500 V e V = 0 no infinito?

28. Considere duas esferas condutoras 1 e 2, separadas por uma grande distância,a segunda tendo o dobro do diâmetro da primeira. A esfera menor possui inicialmente uma carga positiva q e a maior está inicialmente descarregada. Agora você liga as esferas com um fio fino e longo. (a) Como estão relacionados os potenciais finais V₁ e V₂ das esferas?(b) Quais as cargas finais q₁ e q₂ sobre as esferas, em termos de q?(c) Qual a razão entre a densidade superficial de carga final da esfera 1 e a esfera 2?

29. Duas esferas metálicas, cada uma com raio de 3,0 cm, possuem uma separação de 2,0m de centro a centro. Uma delas possui uma carga de + 1,0 x 10^-8C; a outra possui uma carga de -3,0 x 10^-8C. Suponha que a separação é grande o suficiente em relação ao tamanho das esferas para nos permitir considerar a carga sobre cada uma delas sendo distribuída uniformemente(as esferas não afetam uma a outra. Com V = 0 no infinito, calcule (a) o potencial no ponto médio entre seus centros e (b) o potencial de cada esfera.